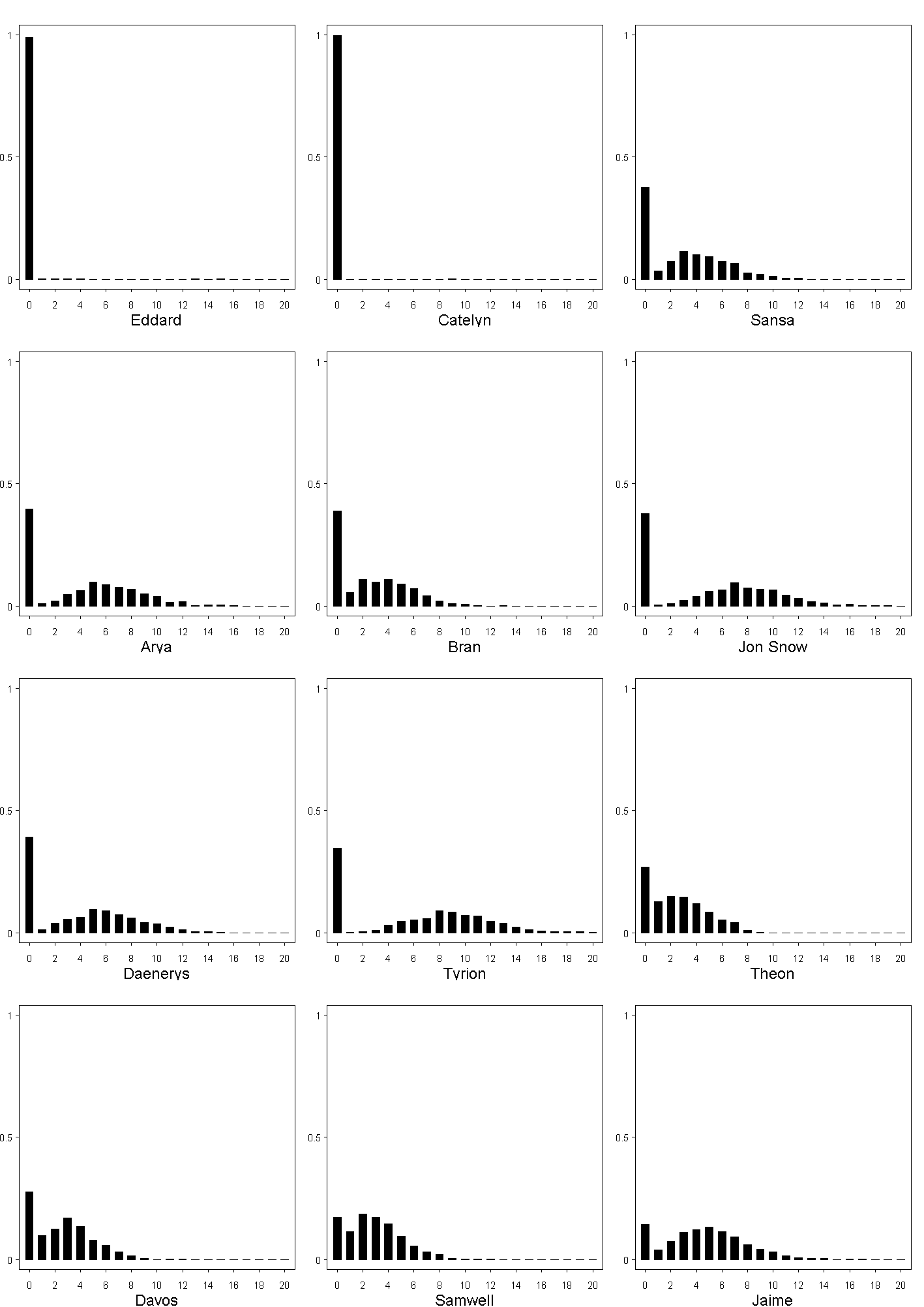
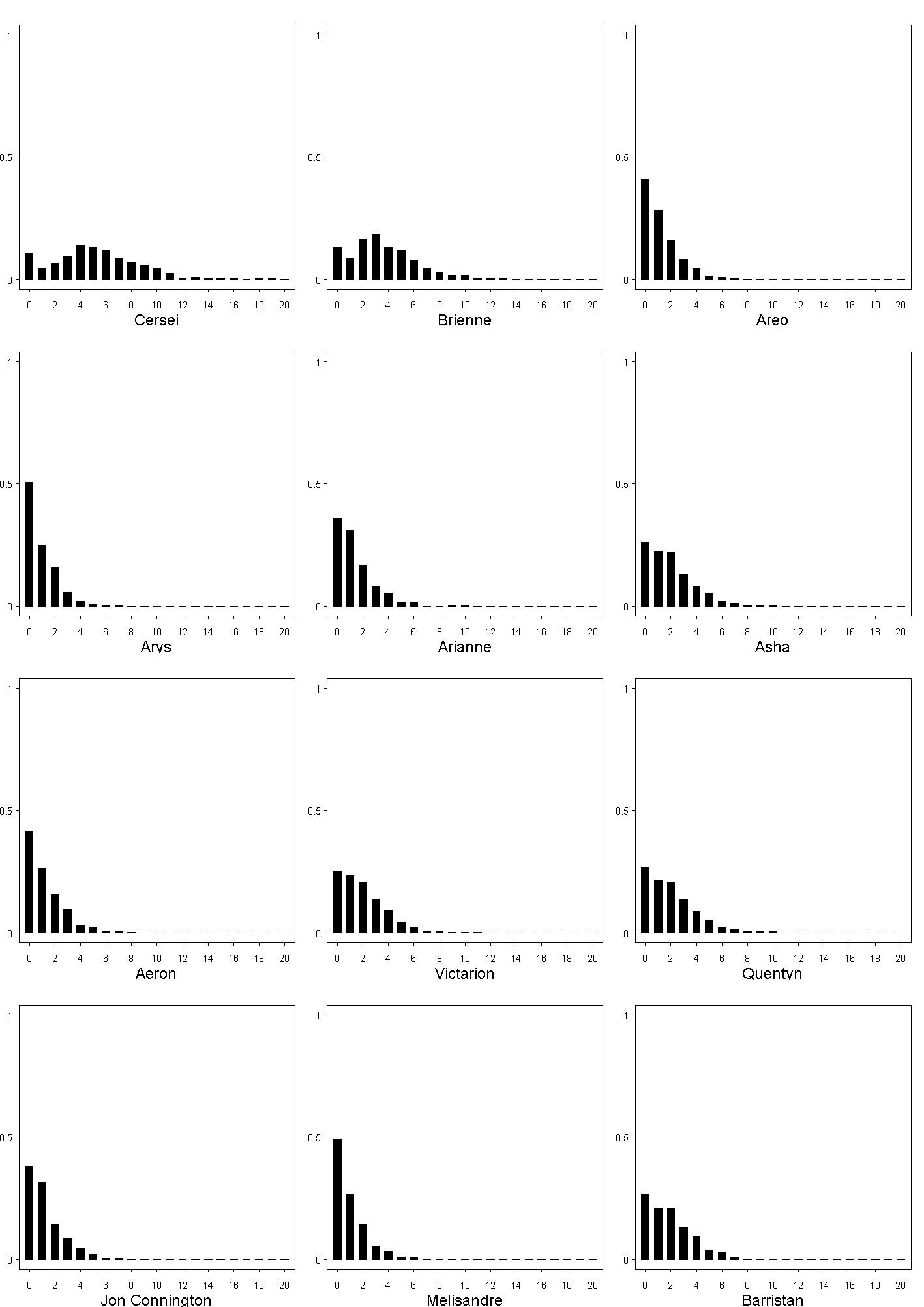
What's this? You are claiming that we can use Bayesian statistics to predict Game of Thrones?
Probably not, no.
But we can try?
Yes!
Explain how.
We have a matrix showing how many chapters in each of the existing novels was narrated from the point of view of each character, and we can fit
a statistical model to that, and try to use the model to predict how many chapters will be told from the point of view of each character in
future novels.
What's the model?
It's a hierarchical model. The number of point-of-view chapters for each character follows a Poisson distribution between certain times, and those
times themselves follow a different underlying distribution. To put it more simply, the number of each character's point-of-view chapters
fluctuates randomly around a certain level, unless the character hasn't appeared yet or has ceased to appear.
So, to put it more simply, the model is: "predict that the character will have about the same number of chapters as they had in the last book,
unless they are dead." What's so impressive about that?
The advantage of using a statistical model is that we can say how uncertain we are about our prediction. For example, anybody could predict that
when a die is rolled, it might be a three. The kind of prediction we want to make is something like: "it has a one in six chance of being a three"
or even better, "it has a one in six chance of being any of the values between one and six." By
I see, a bit like a bookmaker might do for a horse race?
Yes, exactly.
So you could use the model as a guide for betting?
That would be very unwise, because the model does not take events in the books into account at all. Its only input is the number of point-of-view
chapters for each character. To get the most accurate predictions, you might combine the output of a model with common-sense
predictions made by fans of the books.
That's a bit disappointing. I thought predictive modelling was all about big data sets, text mining, sentiment analysis,
support vector machines and that
sort of thing?
Absolutely, all that stuff is very useful. But the aim of this particular project is to see how well we can do at making probabilistic
predictions from a very small data set.
How can you measure the model's performance?
It won't be possible until The Winds of Winter is published, but we can check via simulation that the model is fitted correctly and we
can make a tentative attempt at validation by seeing how it would have predicted earlier novels in the series.
Can I see the model's predictions?
Yes, the posterior predictive distributions for the characters are shown below,
but since this would give away major spoilers for all five of the existing books, you can reach them
by clicking the following thumbnails (they are in png format.)
[Asked by a mathematician friend] I don't see how you can treat the number of point-of-view chapters as random since it completely
depends on the whim of George R. R. Martin, the author of the books.
Randomness is a way of expressing our ignorance about an event rather than a statement about the process which underlies it. For example, if we
know the exact physcial conditions under which a coin is flipped, it is possible to calculate which way up it will land, so in this sense a coin
flip is not random either. Using probability is one way of expressing the fact that we are ignorant of those conditions.
This all seems rather frivolous. Is there a serious side to this work?
I believe that statisticians ought to be more willing to test
their models by making predictions about things that haven't happened yet. It is often said that models can be used either for explanation or
prediction, where "explanation" means that the chosen model could plausibly have generated the observed data.
There are many examples of models which predict well but do not explain. It also makes sense that
it might be a good idea to trade off some predictive ability in exchange for a model which is easier to understand and analyse.
But I cannot currently see how a model which "explains" but does not predict is any better than superstition.
But your criterion for choosing the model was that it could have generated the observed data.
So you're saying that if the model's predictions are no good then it's the fault of statistics?
Not necessarily. It could be that it is a poor choice of model and some other model would do better.
Where can I get more details and further predictions?
In this paper (pdf) Section 1 of the paper is intended to be accessible to a general audience. The paper also contains
spoilers for all five of the existing books.
I am sceptical or curious. Can I see the code?
It is written in R
The truncnorm package must be installed
in order to get exactly the same figures as in the paper.
The code has been moved to a Github repo here.